In practice, most mathematicians choose the journals to submit their research papers based on an informal sense of "reputation" that exists in the mathematical community. Essentially, one talks to their friends and colleagues to get a sense of how journals fall into an "excellent", "good", "fair", and "bad" stratification, and one also asks others for their opinions on which is the better of two among various pairs of journals.
Despite the prevalence of this informal notion of reputation, there have also been efforts to quantify the quality of scientific journals in terms of more objective measures, such as metrics based on citations to articles in the journal. The first attempt at doing so was the Impact Factor, proposed by Eugene Garfield in 1955 and first computed and published by Garfield's Institute for Scientific Information in 1964. (The Institute for Scientific Information was later purchased by Thomson in 1992, and now owned by Thomson Reuters.) For decades after its inception, the Impact Factor was the exclusive metric used to evaluate scientific and mathematical journals. Despite its predominance, there have been several criticisms of Impact Factor within the scientific community, including assertions that its reflection of a journal's quality is exaggerated as well as concerns regarding corporate influence. Despite this, there have been essentially no alternatives to challenge the Impact Factor's monopoly until the past decade. Once challenged, however, the floodgates have opened, and in the past 10 years there has been a proliferation of metrics proposed and published as alternatives to Impact Factor. Like the Impact Factor, all of these metrics are based solely on citations to articles published by the journal. However, they use different algorithms to compute how citations contribute to a journal's assigned score, and they use different sources for the data fed into the algorithm.
In 2005 Jorge Hirsch proposed one of the first alternatives to the Impact Factor, now known as the h-index in his honor, in a paper published in the Proceedings of the National Academy of Science. In 2007 Carl Bergstrom and Jevin West, professors at Washington University, established the Eigenfactor Project to compute and publish the Article Influence Score, a new metric based on the PageRank algorithm and using data provided by Thomsen Rueter's Web of Science. In 2008 the company Scimago, in partnership with Elsevier, introduced and began publishing a new metric called the Scimago Journal Index, which is computed similarly to the Article Influence Score, but using data from Elsevier's Scopus database. In December 2016 Elsevier launched a new metric called CiteScore as an alternative to the Impact Factor. In addition to all of these, the American Mathematical Society now publishes their own metric, called a Mathematical Citatation Quotient, using an algorithm similar to Impact Factor and CiteScore, but with data coming from the MathSciNet database.
Navigating and interpreting these metrics can be an exercise in confusion and frustration. The following is meant as a brief introduction to these metrics, including the algorithms used, the databases that supply citation information, and the various companies and other organizations that are involved.
A bibliometric index is a number produced from an algorithm for the purposes of comparing journals, books, or other publications. Scientific and mathematical journals are often assessed using a particular kind of bibliometric index, known as a citation index, which is based on the citations to articles published by the journal. Higher numbers are typically better, and the implicit idea is that the more a work is cited, the better that work is. (Of course, we can all think of specific situations where this is not true, and we can also expect there will be ways these numbers can be "gamed" and artificially inflated.)
It is important to remember that a citation index provides a single number intended to summarize "how much" a journal's articles are cited. Citation indices are often used as a proxy for the "impact", "quality", "influence", or even "excellence" of a journal. However, it is open to debate how closely a citation index correlates with these qualities. One should also keep in mind the adage "garbage in, garbage out" whenever working with algorithms. Unfortunately, it is common for people to overemphasize the usefulness of citation indices. This is due, in no small part, to the fact our human minds prefer to reduce the complicated comparison of multidimensional attributes to simply determining which of two numbers is larger.
The reality of measuring the "excellence" of a journal is much more complicated and subtle than assigning a single number via an algorithm. While citation indices may be a measure of journal excellence, it is probably best to consider them as providing insight into one particular aspect of that excellence -- specifically, how many authors are aware of the work in the articles published by the journals and influenced enough to cite it. Since no one citation index will give a completely accurate measure of this influence, it is a good idea to look at multiple citation indices in order to gain different perspectives and obtain a more wholistic picture of a journal's influence as measured by citations.[1]
Finally, one should keep in mind that the numerical value of a particular citation index can vary dramatically from one discipline to another. This can be due to the nature of research in the discipline itself or a consequence of the "culture of citation" that has evolved in that discipline. Because of this, it is usually meaningless to compare the citation index of a mathematics journal to the citation index of a journal in another discipline, such as biology, chemistry, or physics. In general, mathematics journals tend to have very low citation indices compared to other disciplines. For example, the best mathematics journals tend to have impact factors that are an order of magnitude smaller than the best biology journals. Likewise, pure mathematics journals tend to have lower citation indices than applied mathematics journals. Consequently, one needs to take care even when comparing mathematics journals that publish different kinds of mathematics.
With analyzing and interpreting a particular citation index, there are (at least)
three consideration to keep in mind:
One should always identify and evaluate the motivations of those providing information. This is particularly relevant for citation indices, since many are currently produced by companies with inherent bias or conflicts of interest. It is, of course, better if citation indices are calculated and reported by impartial entities. It is also preferable to have data that can be accessed by third parties (even after paying a fee) so that reported calculations can be reproduced and verified. One should never forget that the overriding goal of a company is to make money. When financial interests come into play, the truth will be compromised. In the pursuit of profit, companies may be incentivized to promote their particular metrics as being the best, charge for access to the citation indices they produce, or restrict access to their data. It is also not out of the question that some companies may lie. Much like the rise of predatory journals in recent years, disreputable companies have emerged that produce falsified citation indices.
Where does the citation data used by the algorithm come from? Who collected this data, and who decided what (and what is not) included in it? How complete and accurate is this database? Who has the ability to access the database? Can the data be independently confirmed?
How exactly is this citation index calculated from citation data? It is best if one can read and understand the algorithm directly, and the more transparent the algorithm, the better. A "black box" that mysteriously produces a number from data fed into it is largely meaningless and also vulnerable to manipulation. Moreover, as the principle of Occam's razor asserts: in the absence of other factors, a simple algorithm is preferred over a complicated one.
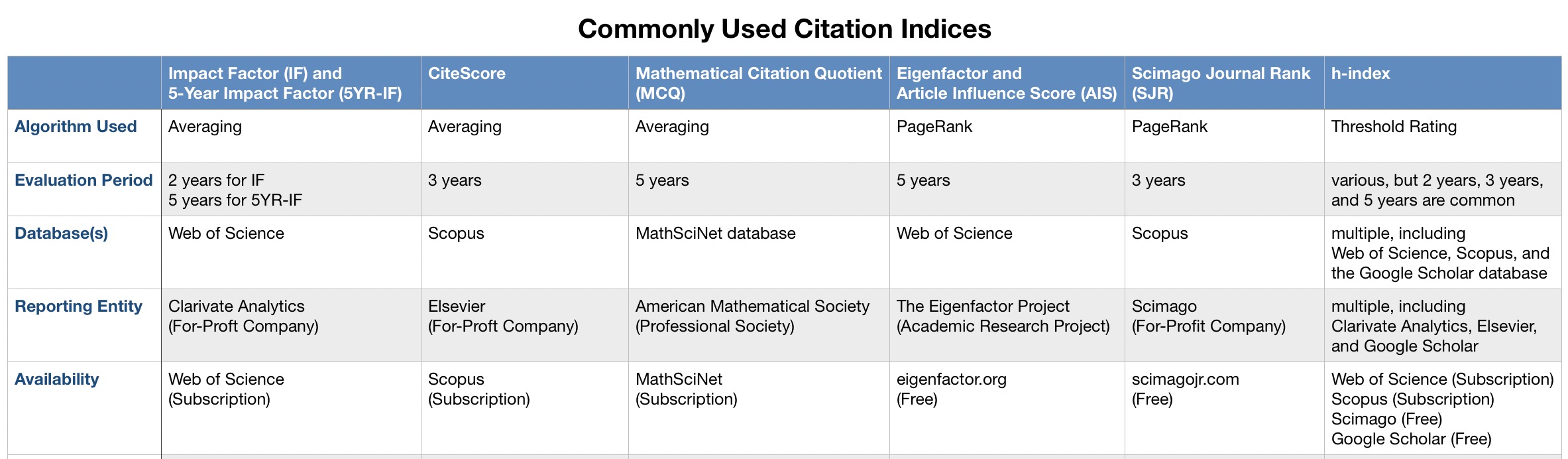
We shall compare popular citation indices for mathematics journals, addressing the three considerations above as we do so. The following table provides a useful reference as we examine each of the citation indices, and as we compare and contrast them.
IF2017 = (# of citations in 2017 to articles published by J during 2015--2016) / (# of articles published by J during 2015--2016)
The number IF2017 may be interpreted as the average number of citations each article published by journal J in 2015 and 2016 received in the year 2017. Of course, the value of impact factor depends on how one defines "article" as well as how one defines "citation". Details on these definitions can be found in the Wikipedia article on Impact Factor.
Impact Factors are reported in the Journal Citation Reports (JCR), an annual publication by the company Clarivate Analytics. One can independently verify the number of citable items for a given journal on the Web of Science. However, the number of citations is extracted not from the Web of Science database, but from a dedicated JCR database, which is not accessible to the general public. Consequently, the commonly used "JCR Impact Factor" is a proprietary value, which is defined and calculated by Clarivate Analytics and cannot be verified by external users. To emphasize their ownership, Clarivate Analytics even requires a particular form for references to their proprietary values:
Clarivate Analytics also publishes 5-Year Impact Factors. The 5-Year Impact Factor is similar to the Impact Factor, except it is calculated over five years rather than two. Specifically, one adds up the number of citations by articles in the given year to articles published by journal J during the preceding five years, divided by the number of articles published by journal J in that preceding five-year period. For example, given journal J, the 5-Year Impact Factor for 2017 for journal J is equal to:If you plan to cite JCR, we require that references be phrased as “Journal Citation Reports” and “Journal Impact Factor,” (not just “Impact Factor”) and, the first time they are mentioned, they must also be acknowledged as being from Clarivate Analytics. For example, “Journal Citation Reports (Clarivate Analytics, 2018).” --source: Clarivate Analytics announcement.
5YR-IF2017 = (# of citations in 2017 to articles published by J during 2012--2016) / (# of articles published by J during 2012--2016)
The number 5YR-IF2017 may be interpreted as the average number of citations that articles published by journal J in the 5-year period 2012--2016 received in the year 2017. One can also view the usual Impact Factor as a 2-Year Impact Factor.
CiteScore is computed in the same way as the Impact Factor, but the average is
taken over the prior three years and uses Scopus (Elsevier’s abstract and citation database)
rather than Clarivate Analytics' JCR database. Thus the formula for the the 2017
CiteScore of journal J is
CS2017 = (# of citations in 2017 to articles published by J during 2014--2016) / (# of articles published by J during 2014--2016)
where citation data is taken from Scopus.
The CiteScore metric was launched in December 2016 by Elsevier as an alternative to the predominantly used JCR Impact Factors. Like the JCR Impact Factor, CiteScore is a proprietary value and although one can independently verify the number of citable items for a given journal on Scopus, the number of citations comes from a private database. Since Clarivate Analytics and Elsevier are both companies with the goal of making money, it is accurate to view the Impact Factor and CiteScore as competing products.
We've already mentioned two differences between Impact Factor and Cite Score: (1) Impact Factor uses citations collected from the previous 2-year and 5-year periods, whereas CiteScore uses citations from the previous 3-year period. (2) Impact Factor uses the Clarivate Analytics' JCR database, while Cite Score uses Elsevier’s Scopus database. There is another important difference: the definition of the "number of publications" or "citable items". While JCR excludes certain items it considers to be minor because they make very few citations to other articles (e.g., editorials, notes, corrigenda, retractions, discussions), CiteScore counts all articles without exception. As a result, CiteScore values are typically lower than Impact Factors, due to dividing by a larger number in the denominator. In fact, it is not unusual for a CiteScore value to be less than half of an Impact Factor due to so many additional items being counted as articles.
CiteScore values of journals are calculated by Elsevier and published on Scopus. They are available to all Scopus subscribers.
The Mathematical Citation Quotient (MCQ) is MathSciNet's alternative to the Impact Factor. The MCQ of a journal is computed over a 5-year period using the same formula as for the 5-Year Impact Factor, but with MathSciNet data in place of Clarivate Analytics' JCR database. MathSciNet is supported by the American Mathematical Society, and the citation data used to compute the MCQ is transparent and visible to anyone with access to MathSciNet. Searching for a journal on MathSciNet will display a page containing a profile for the journal that includes the MCQ with links to all the relevant citation data in the MathSciNet database.
The Eigenfactor Score is computed using a variant of PageRank, the same algorithm used by Google to rank websites for searches. The basic idea is to account for not only quantity, but also quality, of citations. In particular, a citation from an article in a journal with a high score contributes more than a citation from an article in a journal with a lower score. This algorithm can be made precise and the theoretical background can be understood by anyone with undergraduate-level knowledge of Linear Algebra. (For a readable account, see Ch.4 of "Google's PageRank and Beyond" by Amy N. Langville and Carl D. Meyer or visit the Wikipedia article on PageRank.) Moreover, computing the score for journals amounts to calculating an eigenvector for a connectivity matrix determined by the network of citations. Hence the name Eigenfactor Score.
Eigenfactor Scores are considered more robust than Impact Factors. While a journal with a few citations from highly influential authors may have a low Impact Factor, its Eigenfactor Score is typically higher. Unfortunately, unlike the situation with a website where simply adding more pages to the site doesn't usually influence the number of incoming links, larger journals will have higher Eigenfactor Scores due to publishing more articles. Eigenfactor Scores grow linearly with the size of a journal (e.g., doubling the size of a journal and number of articles will roughly double the Eigenfactor Score). The Article Influence Score is meant to account for this, and it is defined as the Eigenfactor Score divided by the number of articles published by the journal, which is then multiplied by a fixed scaling factor. The Article Influence Score is a number that reflects the influence of the average paper in the journal. Eigenfactor Scores and Article Influence Scores are computed using citation data from the previous five years.
The Eigenfactor Project computes and publishes Eigenfactor Scores and Article Influence Scores on the website eigenfactor.org, where they are freely available. The algorithm they use is described in full detail with pseudocode and source code also avaiable. The data that the Eigenfactor Project uses comes from Thomas Reuters' Web of Science and the JCR database owned by Clarivate Analytics.
The Scimago Journal Rank is a metric similar to the Article Influence Score. It is computed by Scimago Lab, a for-profit company that works jointly with Elsevier. The algorithm for SJR uses PageRank to determine an "average prestige per article score" similar to how the Eigenfactor Project computes the Article Influence Score. Scimago makes its algorithm for computing SJR publicly known. However, whereas the Article Influence Score uses the past five years of citations from the the JCR database owned by Clarivate Analytics, Scimago instead uses the past three years of citations from Elesevier's Scopus database to compute the SJR. Scimago makes the SJR values freely available on the Scimago website.
The h-index is a count of the number of articles exceeding a certain threshold. Specifically, the h-index of a journal is defined to be the maximum value N for which the journal has published N papers that have each been cited at least N times. So, for example, suppose we want the h-index for a 3-year window for journal J. We would ask first whether there is at least 1 publication in journal J during this window with at least 1 citation. If the answer is "yes", we then ask whether there are at least 2 publications in journal J during this window that each have at least 2 citations. Continuing, the last integer N for which we can answer "yes" to the question "Are there N articles in the journal each with at least N citations?" is the h-index of journal J for this 3-year window. The h-index also called the Hirsch index or Hirsch number, after its creator Jorge Hirsch, and it is sometimes also capitalized as H-index. Hirsch first proposed the index in a 2005 paper published in the Proceedings of the National Academy of Science.
Many different entities calculate h-indices, and each entity makes its own choice for the window of time used as well as the database from which citation data is drawn. Typical values used for the window of time are 2 years, 3 years, or 5 years. Common choices for the database are Web of Science, Scopus, Google Scholar, and MathSciNet. The value of the h-index will, of course, depend on both the window chosen and which database is used. So one should use care when comparing h-indices computed by different sources.
Both Web of Science and Scopus allow users to search for a journal's h-index and set the desired publication window as part of the search. Scimago publishes a 3-year h-index calculated from Scopus data that is freely available on their website. Google Scholar publishes what it calls an h5-index, which is the h-index using a 5-year window with data used from the Google Scholar database.
[1] Of course, the reality of a struggling academic is that when looking at citation indices, you
may be doing so to maximize perception of excellence, rather than attempting to measure excellence
itself. For instance, if you want to impress a hiring, tenure, or
promotion committee that places emphasis on certain metrics, it makes sense to
maximize those metrics when choosing the journals you submit your work to --- particularly
if doing so doesn't compromise any aspects of your research or its dissemination.